4.8 Random Walks & Pagerank

Consider the following random-walk graphs:

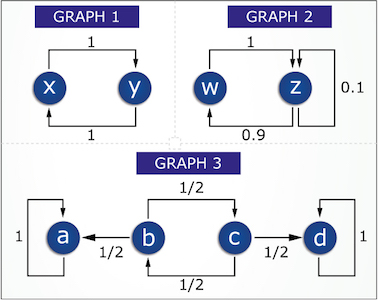
1. If you start at node \(w\) in graph 2 and take a (long) random walk, does the distribution over nodes ever get close to the stationary distribution? Try a few steps to see what is happening.
   Exercise 1

     Yes 

     No 
2. How many stationary distributions are there for graph 3?
   Exercise 2

     0 

     1 

     2 

     4 

     \(2^4\) 

     infinitely many 
3. If you start at node \(b\) in graph 3 and take a (long) random walk, the probabililty you are at node \(d\) will be close to:
   Exercise 3

    \(0\) 

     \(\left(\frac{1}{2}\right)^n\) 

    \(\dfrac{1}{4}\) 

    \(\dfrac{5}{16}\) 

     \(\dfrac{1}{3}\) 

     \(\dfrac{1}{2}\) 

     \(\dfrac{2}{3}\) 

     \(1\) 
   CheckShow Answer